Syntax and semantics

Our first goal in this course is to understand the language of programming languages. That is to say, a formal system for describing the different components of a programming language. As a running example, we will start with the language of arithmetic, e.g. expressions like $1 + 6 * 3 / 2$. To fully characterize the language of arithmetic, we need to answer three questions:

• Syntax: What is the structure of an arithmetic expression?
• Static semantics: What subset of arithmetic expressions have meaning?
• Dynamic semantics: What is the meaning of a given arithmetic expression?

Syntax

Languages begin with primitives, or objects that represent atomic units of meaning. Arithmetic has only one primitive, numbers, while most programming languages have many primitives like characters, booleans, functions, and so on. Natural language has nouns, adjectives, and verbs.

The fundamental function of a language is to define structure over primitives by composition. Composition means any kind of operation or structure that uses or relates objects. In natural language, we make meaning with sentence structures, e.g. by subject-verb-object composition. In arithmetic, composition consists of binary operators that combine two numbers together. We can write down the structure of arithmetic as a context-free grammar:

A grammar is a meta-linguistic concept, a tool for describing language structure. The specific grammar notation shown is a variant of the canonical Backus-Naur Form for specifying context-free grammars. Each rule (or “production”) specifies different ways of generating a kind of structure. You can read it as: “a binary operator $\hoplus$ can be one of four symbols: $\hadd$, $\hmin$, $\hmul$, or $\hdiv$. An expression $e$ can be one of two things: a number $n$, or a combination of two sub-expressions $e_1 \hoplus e_2$.” For example, $1$, $1 \hadd 2$, and $2 \hmul 3 \hdiv 1$ are all syntactically valid expressions, while $2 \hmul \hadd 1$ is not.

The symbols $e, n, \hoplus$ are metavariables in that they are placeholders for syntax, not actual variables within the language being described. That is, $1 \hadd e$ is not an arithmetic expression because our arithmetic language does not have a notion of variables. (Yet!) But we can say $1 \hadd 2$ is an arithmetic expression where $e_1 = 1, e_2 = 2, \hoplus = \hadd$.

Syntax trees

We must be careful when discussing structure to understand the true shape of our language. When communicated in text, an arithmetic expression looks like a sequential string of characters, e.g. $1 \hadd 2 \hmul 3$, but that is merely a limitation of text as a medium. Context-free grammars describe tree structures, and the linear text is implicitly describing this tree:

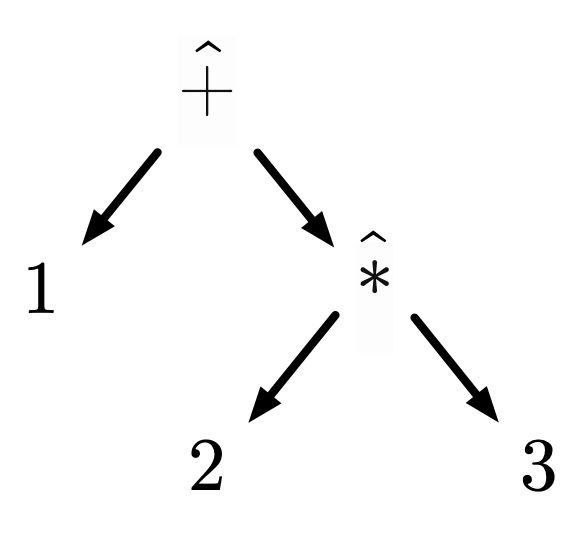
From this perspective, we can define syntax as establishing the basic structure of a language. Syntax is not just about curly braces vs. whitespace or char vs uint8_t. This is sometimes distinguished as a language’s abstract syntax versus its concrete syntax, where abstract refers to structure and concrete refers to symbols. A language could have multiple concrete syntaxes for the same abstract syntax, e.g. our diagram and text representations of arithmetic. The tree corresponding to a piece of syntax is subsequently called an abstract syntax tree, or AST.

Trees and context-free grammars are often treated as fundamental to programming languages. But it is an interesting and open question of alternate representations for language syntax. For example, if we introduce variables into our arithmetic language:

And then given have a program like $(\letv{x}{1}{x + x})$, the essence of the program’s structure is no longer strictly tree like, since the subexpression $x + x$ depends on the parent expression. Many functional languages implement term graph rewriting to take advantage of this fact.

Ambiguity and precedence

The task of parsing a string into a tree is often underspecified in the face of an ambiguous grammar. In our grammar, the string $1 \hadd 2 \hdiv 3$ could be parsed as $(1 \hadd 2) \hdiv 3$ or $1 \hadd (2 \hdiv 3)$. Carefully designing grammars to be unambiguous is an important task for compiler implementors, e.g. see CS 143 Introduction to Parsing.

In this class, our primary concern when discussing grammars is to understand the simplest essence of our language structure. Hence we will not try to make the grammar more complex to avoid ambiguities, instead we will state (in English) precedence and associativity rules. For arithmetic, you can assume standard associativity and precedence (PEMDAS) rules.

Sources of meaning

In general, it can be difficult to talk about languages, because we necessarily have to use language in order to communicate linguistic concepts. We will be particular on a few details in order to clarify certain distinctions. Here, we use the hat notation on the binary operators to make it absolutely clear that the symbols $\hadd$ and friends have absolutely no meaning. They are icons with no semantics, and we merely have a grammar that determines how those symbols can be put together. They are not the same as the $+, -, *, /$ symbols with their commonly associated semantics in standard arithmetic.

Semantics

Syntax defines the set of allowable forms in our language, the structure of our domain. The next step in defining a programming language is to establish its semantics and properties. How do we talk about what an arithmetic expressions means, or whether one makes sense in the first place?

Language semantics has a rich history spanning logic, computer science, philosophy, linguistics, and many other fields. In natural language, we often think about semantics hierarchically—assigning meaning to the phrase “Will went to the store” starts with understanding “Will”, “went”, and “store”, then combining those meanings in a subject-verb-object composition. This produces an abstract meaning that is identical to a different concrete syntax like “Will去了商店”. This style of understanding meaning is close to denotational semantics.

For programming languages, we are more interested in the notion of computation as semantics. For example, our goal is not to assign semantics to the string "hello"—it is up to the programmer to decide how to interpret the contents of a string in a given application. Rather, a program is a structure that can be computed, e.g. "hello" + " world" reduces to "hello world". More generally, given a language that defines expressions, our goal is to define a semantics that can reduce an expression to a primitive form. Somehow we should get from $1 \hadd 2 \hmul 3$ to $7$.

This idea of computation as reducing expressions may seem a little foreign. In the Turing languages you’re used to, a program consists of a series of statements. For example, a simple C program:

int main() {
  FILE* f = fopen("/tmp/foo");
  fwrite(f, "bar");
  fclose(f);
  return 0;
}

What can we say this program “means”? Surely it means more than just its return code—it’s the effects of running the program, e.g. writing to a file, that are the important parts. Each statement in this program has an effect, but does not represent an object/datum/value in of itself. The line return 0 is purely control flow, it does not have a value.

By contrast, expressions have values. Church languages are expression-oriented in that an entire program is a single expression, so a program represents a single value. In the arithmetic language, any program (arithmetic expression) corresponds to a single number resulting from its computation. It should seem weird that a complex program with many effects could be represented this way, but we’ll dive into that correspondence down the line.

Operational semantics

We will define a formal notion of computation for expression languages through a small-step operational semantics. For any given expression $e$, it can be in one of two states: either it’s reducible, meaning a computation can be performed, or the expression is a value, meaning it’s reached a final form. We formalize these states as logical judgments, written as $\steps{e}{e'}$ for “$e$ steps to $e'$” and $\val{e}$ for “$e$ is a value”. We then define a formal system for proving these judgments about expressions. Below is a complete operational semantics for arithmetic:

Each of these lines represents an inference rule, which you can read as a vertical implication. $\frac{a}{b}$ is the same as $a \implies b$, or “if the top is true, then the bottom is true.” So the first rule is an axiom reading as “unconditionally, any number $n$ is a value.” The second rule reads as “if $e_1$ steps to $e_1'$ then $e_1 \hoplus e_2$ steps to $e_1' \hoplus e_2$”. If a rule contains multiple premises separated by spaces, they are all required to prove the conclusion (i.e. AND, not OR).

Like much of abstract mathematics, PL theory makes use of implicit context to simplify its notation. For example, in the D-Num rule, we rely on the fact that $n$ was earlier established to represent numbers to mean that the D-Num rule only applies to numbers. Moreover, the rule is implicitly quantified over all numbers, i.e. we could formally write the rule as:

$$\forall n \in \mathbb{N} . \ir{D-Num}{}{\val{n}}$$

Similarly, D-Left has an implicit $\forall e_1, e_2 \in \mathsf{Expression}$ in the front. If you’re ever confused about unstated assumptions in a rule, make sure to ask!

Now that we can read the rule notation, let’s revisit what they’re saying about arithmetic computation semantics. The first rule is establishing a termination condition for arithmetic programs: once we’re reached a number $n$, that’s value so we’re done. The next two rules define an order of operations, but not in the traditional sense of PEMDAS. Rather, they answer the question: if I have an expression with two reducible subexpressions like $(1 \hadd 2) - (4 \hdiv 2)$, which subepxression do we reduce first? For arithmetic, the answer is (unsatisfyingly) that it doesn’t matter. Our language is so simple that we will always arrive at the same value under either reduction strategy. So we arbitrarily pick to reduce the left expression first. Hence, the D-Left rule says if the left side can be reduced, then reduce it. D-Right says that if the left side cannot be reduced and the right side can, then reduce the right side.

Finally, we arrive at $\text{D-$\oplus$}$. This rule says, when we have a binary operator $\hoplus$ with two subexpressions that are both numbers, then perform the corresponding arithmetic operation. This is notationally expressed by removing that hat, implicitly assuming that if $\hoplus = \hadd$ then $\oplus = +$ and so on. What does this mean, and why does it work? Essentially, we’re saying: our language’s semantics exist within an external theory of arithmetic binary operators. So we assume that, elsewhere, we’ve formally defined how to compute $n_1 + n_2$, and we’re using that “module” in our language’s semantics. The only real value of our formal language on top of that theory is to define an order of operations for composite expressions.

We will see next week how to define a theory of arithmetic internal to a language, meaning that we can build up what $n_1 + n_2$ means purely from the language’s primitives. In the meantime, think about it yourself—how would you formally define the behavior of addition in a non-circular way? As a hint, you will need to rethink our representation of numbers. For example, what property defines that 5 is 1 more than 4?

Term reduction proof

To see these rules in action, let’s try to prove a simple reduction: $1 \hadd 6 \hmul 3 \hdiv 2$ evaluates to 10. We will use the syntax $\evals{e_1}{e_2}$ to mean “$e_1$ reduces to $e_2$ after zero or more steps”, so our proof goal is $\evals{1 \hadd 6 \hmul 3 \hdiv 2}{10}$. The full evaluation will take many steps, so we will just attempt to prove the first reduction. Following our precedence rules, we will start with $e_1 = 1$, $e_2 = 6 \hmul 3 \hdiv 2$, and $\hoplus = \hadd$. Using our bar notation, we can start our proof like this:

This visual structure says: our goal is to prove that the expression steps to something. But we’re not sure what it steps to, or what rule to apply. The proof strategy here is fairly simple: brute force search. There are four possible rules that could possibly apply to our term. We can look at each one in turn to decide which is applicable.

• D-Num: the expression is not a number, so D-Num does not apply.
• D-Left: this rule applies if $e_1$ can step. $e_1 = 1$ and $\val{e_1}$, so D-Left does not apply.
• D-⊕: this rule applies if both $e_1$ and $e_2$ are numbers. $e_2$ is not a number, so D-⊕ does not apply.
• D-Right: this rule applies if $e_1$ is a value (it is), and if $e_2$ can step. This seems like it might apply, so we can begin our proof here.

Now you can start to see the full proof strategy. Given the final goal, we recursively prove its assumptions until we reach axioms. Once every part of the proof tree is fully justified, we have a complete proof. Repeatedly applying this proof strategy to our subexpression, we ultimately arrive at the following proof:

This is only the first reduction—we would need to similarly prove that $\steps{1 \hadd 18 \hdiv 2}{1 \hadd 9}$ and $\steps{1 \hadd 9}{10}$ to complete the full proof. I’ll leave these steps as an exercise to the reader.

What if the D-Right rule did not apply at the bottom of the proof? This would mean that our operational semantics for arithmetic are unsound, i.e. there are reducible expressions (not values) for which no step can be proved. In a real world context, this means our language has undefined behavior, and a compiler/interpreter could choose to do arbitrary things to the expression. This gets to our original second question: what subset of arithmetic expressions have meaning? For now, the answer is “all of them”, but we will revisit this question next week for languages that require a type system.

Structural induction

The previous section showed how to use our semantics to prove a judgment about a particular expression, i.e. that it stepped to something else. Raising the level of abstraction, let’s now prove something about our language, meaning a universal statement over all possible programs. Specifically, we want to demonstrate that all programs in our language are total or terminating. Informally, this means that each program always evaluates to a value. The program never gets stuck (no rules apply), raises an error, or loops forever (“diverges”). Formally, we can write this theorem as:

Totality of arithmetic: for all expressions $e$, there exists an $e'$ such that $\evals{e}{e'}$ and $\val{e'}$.

Our proof strategy here is different than the previous proof, since we are proving a statement about all expressions instead of a single one. How should we go about doing this? Think back to our grammar and the structure of our language. Each expression is either a primitive (a number), or a composition of sub-expressions. This closely mirrors the structure of an inductive proof: a base case and an inductive case.

Before diving into induction on our language, let’s discuss how we can derive the principles of induction from scratch. When you learned about induction in 103 or elsewhere, you were provided the induction principle for natural numbers:

Induction over natural numbers: $(\forall n \in \mathbb{N} . P(n)) \iff (P(0) \wedge (\forall n \in \mathbb{N} . P(n) \implies P(n+1)))$

This principle allows us to prove a universal statement (proposition $P$) for all natural numbers by showing a base case $P(0)$ and an inductive case $P(n) \implies P(n+1)$. Then you were given an intuitive justification for this principle through diagrams like this:

Despite its creativity, this diagram is not a proof. How can we formally prove the induction principle for natural numbers? This becomes much simpler if we expose the underlying inductive structure of numbers. Specifically, we can use the Peano numerals:

This says “any number is either Z (zero) or the successor (+1) of a previous number.” So for example, $Z = 0$, $S(Z) = 1$, $S(S(S(Z))) = 3$, and so on. Now let’s revisit our induction principle in this alternative number representation:

Now, each part of the induction principle comes more clearly from its inductive structure. If $n = Z$, then we must prove $P(Z)$. If $n = S(n')$, then we must prove $P(n') \implies P(S(n'))$. More generally, any inductive structure comes with a corresponding induction principle. For each element of the structure, if it has no sub-parts, then it is a base case (e.g. zero). If it has sub-parts (e.g. successor), then it is an inductive case. The inductive hypothesis is to assume that the proposition holds on the sub-parts, and prove that the proposition holds for the composition.

This idea is called structural induction, and it generalizes mathematical induction. I cannot overemphasize its importance because this proof technique underlies nearly all theory in programming languages, as inductive structures are extremely common. Knowing this principle of induction principles allows you to use inductive proofs for arbitrary structures that you’ve defined, not just the sanctioned ones you’ve been taught (e.g. natural numbers). Let’s apply this idea to our arithmetic language. Recall that expressions have this structure:

From this grammar, we derive the following induction principle:

This says: a proposition is true for all expressions in our language if it’s unconditionally true for all numbers, and conditonally true for all composite expressions if true for the sub-expressions.

Totality proof

Finally, let’s apply this principle to prove the totality of arithmetic. As a reminder, the theorem:

Totality of arithmetic: For all expressions $e$, there exists an $e'$ such that $\evals{e}{e'}$ and $\val{e'}$.

For this proof, we will assume the following lemma (proving it is an exercise for the reader):

Inversion of arithmetic values: For all expressions $e$, if $\val{e}$, then $e$ is a number $n$.

For totality, we will prove each case in turn.

1. Let $e = n$. Then for $e' = n$, we trivially have $\evals{e}{e'}$, and $\val{e'}$ by D-Num.

2. Let $e = e_1 \hoplus e_2$.

   • Assume totality for $e_1$ and $e_2$. By the induction hypothesis, let $e_1', e_2'$ such that $\evals{e_1}{e_1'}$ and $\evals{e_2}{e_2'}$ and $\val{e_1'}, \val{e_2'}$.
   • By the inversion lemma, $e_1' = n_1$ and $e_2' = n_2$.
   • By D-Left, $\evals{e_1 \hoplus e_2}{n_1 \hoplus e_2}$.
   • By D-Right, because $\val{n_1}$ by D-Num, $\evals{n_1 \hoplus e_2}{n_1 \hoplus n_2}$.
   • Let $n_3 = n_1 \oplus n_2$. Then $\evals{e}{n_3}$ and $\val{n_3}$ by D-Num, so totality holds.

That’s it! We’ve proved totality (termination) for all expressions in our language. As we’ll see next week, as our language grows, we’ll simply add more and more cases to our inductive proof. In terms of proof strategy, the tricky part is usually carefully articulating assumptions in the inductive cases and applying the appropriate lemmas. For example, it seems obvious now that $\val{e} \implies e = n$. However, languages often have more than one kind of value (e.g. numbers and strings), and so the basic inversion lemma would only show that $\val{e} \implies e = n \vee e = s$.